
我們在“深入淺出的學習傅里葉變換”時曾了解到,數學界有過一場“正弦曲線能否組合成一個帶有棱角的信號”的偉大爭議,而這場爭議的男主角自然就是傅里葉和拉格朗日了。當然兩位男主角都沒有錯,劇情也告一段落。
直到1898年,美國阿爾伯特·米切爾森做了一個諧波分析儀,當他測試方波時驚訝的發現方波的XN(t)在不連續點附近部分呈現起伏,這個起伏的峰值大小似乎不隨N增大而下降!于是他寫信給當時著名的數學物理學家吉布斯,吉布斯檢查了這一項結果,隨機發表了他的看法:隨著N增加,部分起伏就向不連續點壓縮,但是對任何有限的N值,起伏的峰值大小保持不變,這就是吉布斯現象。
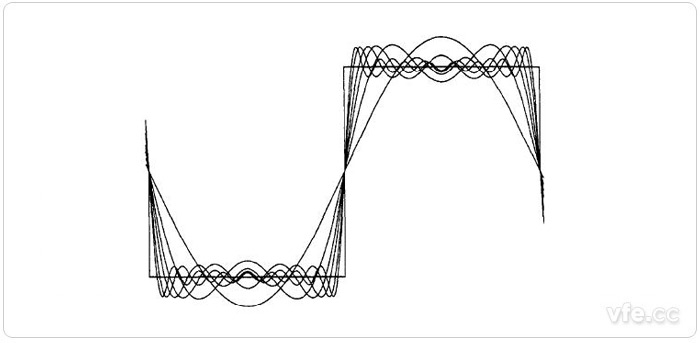
吉布斯現象示意圖
吉布斯現象的含義是:一個不連續信號X(t) 的傅里葉級數的截斷近似XN(t),一般來說,在接近不連續點處將呈現高頻起伏和超量,而且,若在實際情況下利用這樣一個近似式的話,就應該選擇足夠大的N,以保證這些起伏擁有的總能量可以忽略。當然,在極限情況下,近似誤差的能量是零,而且一個不連續的信號(如方波)的傅里葉級數表示是收斂的。
出現吉布斯現象其實是由于傅里葉變換本身有很多成熟的快速算法(如FFT),而且性能接近最佳,但它由于圖像數據的二維傅里葉變換實質上是一個二維圖像的傅里葉展開式,當然這個二維圖像被認為是周期性的。由于子圖像的變換系數在邊界上不連續,而將造成的復原子圖像也在其邊界上不連續。于是由復原子圖像構成的整幅復原圖像將呈現隱約可見的以子圖像尺寸為單位的方塊狀結構,影響整個圖像質量。這就是為什么傅里葉變換在分析方波時在其不連續點上出現吉布斯現象的原因了。
解決吉布斯現象的方法是后來研究出來的離散余弦變換(DCT),即在傅里葉級數展開式中,如果被展開的函數是實偶函數,那么其傅里葉級數中只包含余弦項,再將其離散化可導出余弦變換。
基本思路為:將一個對稱的2N*2N像素的子圖像代替原來N*N子圖像。由于對稱性,子圖像做二維傅里葉變換,其變換系數將只剩下實數的余弦項。這樣就可以消除吉布斯現象了。